Answer:
Following are the responses to the given choices:
Step-by-step explanation:
For point a:
Using the acid and base which are strong so,
moles of
 (from
(from
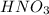 )
)
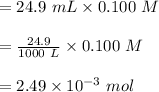
moles of
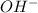 (from
(from
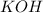 )
)
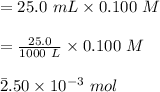

So,
 i.e.
i.e.
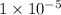 mol of
mol of
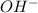 in excess in total volume
in excess in total volume
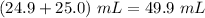 i.e. concentration of
i.e. concentration of
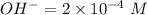
![p[OH^(-)] = -\log [OH^(-)] = -\log [2 * 10^(-4)\ mol] = 3.70](https://img.qammunity.org/2022/formulas/chemistry/college/96sbhe869oha1wmrnszeek7h1njt6620bz.png)
Since,
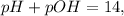
so,
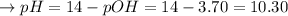
For point b:
moles of
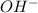 = from point a
= from point a

moles of
 (from
(from
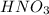 ):
):

1 mol
 neutralizes 1 mol of
neutralizes 1 mol of
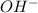
So,
 i.e.
i.e.
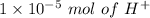 in excess in the total volume of
in excess in the total volume of
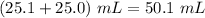 i.e. concentration of
i.e. concentration of

Hence,
![pH = -\log [H^+] = -\log[2 * 10^(-4)] = 3.70](https://img.qammunity.org/2022/formulas/chemistry/college/app168zkzbpawfkccua02hl15wjh5wyakp.png)