Question

What is the probability of flipping a coin 12 times and getting heads 3 times? Round your answer to the nearest tenth of a percent. O A. 5.4% O B. 12.5% O C. 12.1% O D. 19.3% SUBMIT​

Answer 1

Answer: A) 5.4%

==================================

Step-by-step explanation:

We use the binomial probability formula here

P(k) = (n C k)*(p)^k*(1-p)^(n-k)

In this case, there are n = 12 trials and p = 0.5 is the probability of getting heads. The value of k = 3 means we want 3 heads.

So,

P(k) = (n C k)*(p)^k*(1-p)^(n-k)

P(3) = (12 C 3)*(0.5)^3*(1-0.5)^(12-3)

P(3) = 220*(0.5)^3*(1-0.5)^(12-3)

P(3) = 0.0537109375

P(3) = 0.054

P(3) = 5.4%

-----------------

Side note: the n C k refers to the nCr combination formula

`_n C _r = (n!)/(r!*(n-r)!)`

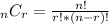
where the exclamation marks mean factorials. You could also use Pascal's Triangle as an alternative for this portion.