Question

Select all the numbers that are irrational

Answer 1

2 Answers:

A)
`-√(5)`

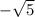
D)
`\pi`

===========================================

Step-by-step explanation:

Choices B and C are rational because we can simplify them to form a fraction of integers.

`-√(49) = -7 = -(7)/(1)`

`√(0) = 0 = (0)/(1)`

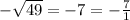
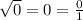
Any rational number is of the form P/Q where P,Q are integers and Q is nonzero.

So we can rule out choices B and C.

---------------

Choice A on the other hand cannot be written as a fraction of integers. The 5 isn't a perfect square, which makes
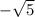`-√(5)` irrational.

The same can be said about
`\pi` which is roughly equal to 3.14; the decimal digits go on forever without a known pattern.

Choice A and choice D are the two answers.

----------------

If we know the pattern of the decimal digits, then we can turn the decimal number into a fraction of integers

The number -0.777, where the 7s go on forever, converts to the fraction -7/9

That means we rule out choice E.