Answer: D) Reflect over x-axis
=======================================================
Step-by-step explanation:
When we do this type of reflection, a point like (1,2) moves to (1,-2).
As another example, something like (5,-7) moves to (5,7)
The x coordinate stays the same but the y coordinate flips in sign from positive to negative, or vice versa.
We can say that
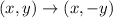 as a general way to represent the transformation. Note how y = f(x), so when we make f(x) negative, then we're really making y negative.
as a general way to represent the transformation. Note how y = f(x), so when we make f(x) negative, then we're really making y negative.
If we apply this transformation to every point on f(x), then it will flip the f(x) curve over the horizontal x axis.
There's an example below in the graph. The point A(2,8) moves to B(2,-8) after applying that reflection rule.