Answer:
B, D, and E.
Explanation:
We are given the graph:
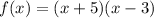
We can expand the equation into standard form:
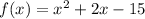
Since the leading coefficient is positive, our parabola curves up. Hence, it has a relative minimum.
The x-intercepts of a function is whenever y = 0. Hence:
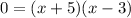
Zero Product Property:
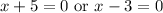
Solve:
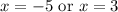
So, our x-intercepts are (-5, 0) and (3, 0).
The y-intercept occurs when x = 0. Hence:
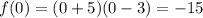
So the y-intercept is (0, -15).
The axis of symmetry is given by:
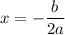
In this case, from standard form, a = 1, b = 2, and c = -15. Hence:
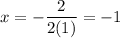
Our axis of symmetry is -1.
Therefore, the correct statements are B, D, and E.