Question

Renna pushes the elevator button, but the elevator does not move. The mass limit for the elevator is 450450450 kilograms (\text{kg}kgstart text, k, g, end text), but Renna and her load of identical packages mass a total of 620\,\text{kg}620kg620, start text, k, g, end text. Each package has a mass of 37.4\,\text{kg}37.4kg37, point, 4, start text, k, g, end text.

Write an inequality to determine the number of packages, ppp, Renna could remove from the elevator to meet the mass requirement.
What is the minimum whole number of packages Renna needs to remove from the elevator to meet the mass requirement?

Answer 1

5 packages and P > 4, 14 or P > 29/7

Explanation:

I did it before

Answer 2

Renna needs to remove at least 5 packages to meet the elevator's 450 kg mass limit. The inequality is
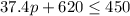`\(37.4p + 620 \leq 450\)`, where p is the number of packages.

Let p be the number of packages Renna could remove from the elevator. The total mass of Renna and the packages is given by the equation:

`\[ 37.4p + m_R \leq 450 \]`

Where
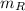`\( m_R \)` is Renna's mass, which is 620 kg.

Substitute the values:

`\[ 37.4p + 620 \leq 450 \]`

Now, solve for p:

`\[ 37.4p \leq 450 - 620 \]`

`\[ 37.4p \leq -170 \]`

Divide both sides by 37.4:

`\[ p \leq -4.55 \]`

Since the number of packages (p) cannot be negative, we take the ceiling of the value (smallest integer greater than or equal to -4.55), which is
`\( p \leq -4 \).`

Renna cannot remove a negative fraction of a package, so she needs to remove at least 5 packages to meet the mass requirement. Therefore, the minimum whole number of packages Renna needs to remove from the elevator is 5.