Answer: Region Q
==========================================================
Step-by-step explanation:
Let's focus on the inequality 4x-2y > 6
Plug in (x,y) = (0,0) to find that...
4x-2y > 6
4(0)-2(0) > 6
0 > 6
This is a false statement. So that means (0,0) is not in the shaded region for 4x-2y > 6. So we'll shade the opposite side of the dashed line to shade regions Q and R (i.e. stuff below the dashed line).
-----------------
Let's check the point (0,0) with the other inequality as well

This is true because 0 is to the right of -20 on the number line.
So we'll shade regions P and Q to represent the solution set for this inequality. These regions are above the boundary line. Points on the boundary are also included.
------------------
To summarize so far, we found that
- regions Q and R make 4x-2y > 6 true,
- regions P and Q make
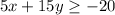 true.
true.
The overlap is region Q which is the final answer
Any point from region Q satisfies both 4x-2y > 6 and
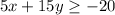 at the same time. A point on the solid boundary line is part of the solution set, but stuff on the dashed boundary line are not solution points.
at the same time. A point on the solid boundary line is part of the solution set, but stuff on the dashed boundary line are not solution points.