Question

You roll two fair dice. Find the probability that the first die is a 6 given that the minimum of the two numbers is a 2.

Answer 1

1/9 = 0.1111 = 11.11% probability that the first die is a 6 given that the minimum of the two numbers is a 2.

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

In which

P(B|A) is the probability of event B happening, given that A happened.

`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Minimum of the two numbers is 2.

Event B: First die in a 6.

Fair dice:

Each throw has 6 equally likely outcomes. Thus, in total, there are
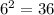`6^2 = 36` possible outcomes.

Minimum of the two numbers is a 2.

(2,2), (2,3), (3,2), (2,4), (4,2), (2,5), (5,2), (2,6), (6,2).

9 total outcomes in which the minumum of the two numbers is a two, which means that:

`P(A) = (9)/(36)`

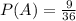
Minimum of the two numbers is a 2, and the first die is a 6.

Only one possible outcome, (6,2). So

`P(A \cap B) = (1)/(36)`

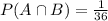
Probability that the first die is a 6 given that the minimum of the two numbers is a 2.

`P(B|A) = (P(A \cap B))/(P(A)) = ((1)/(36))/((9)/(36)) = (1)/(9) 0.1111`

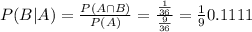
1/9 = 0.1111 = 11.11% probability that the first die is a 6 given that the minimum of the two numbers is a 2.