Question

Consider the quadratic equation 2x² + 72 + k = 0. Which value of k results in the equation having complex solutions?​

Answer 1

Hi there!

`\large\boxed{k> 6.125}`

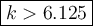
We can use discriminants to determine the value of k for which the equation would have complex solutions. (Those involving i)

If b² - 4ac < 0, then the equation will have complex solutions. Therefore:

Plug in the given values of b and a to solve:

7² - 4(2)(k) < 0

Simplify:

49 - 8k < 0

Solve the inequality:

49 < 8k

6.125 < k

k > 6.125. Anything greater than 6.125 would result in complex solutions.