Answer:
6600ft.² is the correct answer.
Explanation:
Given that,
- Diameter of the Cylindrical tank, d = 60 ft
- Height of the Cylindrical tank, h = 20 ft
- Radius of the Cylindrical tank, r = 30ft.

To Find:
- Area of the Cylindrical tank to be painted.

Solution:
Area of Cylindrical tank to be painted = CSA of the Cylindrical tank + Area of the circle

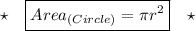
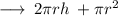
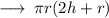
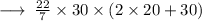
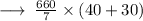
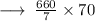
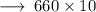
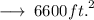
Hence, Area of the Cylindrical tank to be painted is 6600ft.²
_____________________
Additional Information:
