Answer:
Explanation:
Part C: (Explanation with steps)
Let the length of the swimming pool = l feet
And width of the pool = w feet
Perimeter of the pool = 2(l + w) feet
Since, perimeter of the pool = 8 feet
2(l + w) = 80
l + w = 40
l = (80 - w) -------(1)
Area of the pool = Length × width
A(w) = l × w
By substituting the value of l from equation (1)
A(w) = (80 - w) × w
A(w) = 80w - w²
To find the maximum area of the pool we will find the derivative of the function with respect to 'w' and equate it to zero.
A'(w) = 80 - 2w
(80 - 2w) = 0
w =
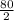
w = 40 feet
Therefore, for width (w) = 40 feet area of the pool will be maximum.
From equation (1),
l = 80 - 40
l = 40 feet
Therefore, maximum area of the pool = l × w
= 40 × 40
= 1600 square feet
Part A:
Function representing area of the pool,
A(w) = -w² + 80w
Part B:
Maximum area of the surface of the pool = 1600 square feet