Question

Find BC
Round to the nearest tenth.
7
140°
B
13

Answer 1

The answer is

Explanation:

This is from khan academy. so You need to watch a video on khan academy to get help.

Answer 2

The length of side BC, rounded to the nearest tenth, is 18.9 units.

To find the length of side BC in the given triangle, we can use the Law of Cosines, which relates the lengths of the sides of a triangle to the cosine of one of its angles. The Law of Cosines states:

`\[ c^2 = a^2 + b^2 - 2ab \cdot \cos(C) \]`

where
`\( c \)` is the length of the side opposite angle C,
`\( a \)` and
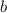`\( b \)` are the lengths of the other two sides, and
`\( \cos(C) \)` is the cosine of the angle C.

From the image, we have:

- Side AB = 13 (between points A and B)

- Side AC = 7 (between points A and C)

- Angle
`\( A = 140^\circ \)`

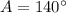
We want to find the length of side BC. Applying the Law of Cosines:

`\[ BC^2 = AB^2 + AC^2 - 2 \cdot AB \cdot AC \cdot \cos(A) \]`

Plugging in the values:

`\[ BC^2 = 13^2 + 7^2 - 2 \cdot 13 \cdot 7 \cdot \cos(140^\circ) \]`

We will calculate this using the cosine of 140 degrees, which we'll convert to radians because Python's cosine function takes radians. The conversion is
`\( \text{radians} = \text{degrees} * (\pi)/(180) \).`

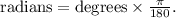
The length of side BC, rounded to the nearest tenth, is 18.9 units.