Question

The difference of the square of a number and 18 is equal to 3 times that number. Find the positive solution.

Answer 1

18 = 3 x 6

Explanation:

If you don't know the difference of the square of a number you can already see that it's telling 18 = 3 times that number so identify the missing number by multiplying 3 times a number.

18 = 3 x ?

18 = 3 x 6

18 = 18

:D

Answer 2

6

Explanation:

Let us start by writing an equation using the variable x.

The square of a number x minus 18 equals 3 times x:

`x^(2) -18=3x`

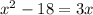
Great! Now let us solve for x by moving the 3x term to the left side of the equation and obtain a quadratic equation:

`x^(2) -3x-18=0`

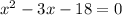
We can use the quadratic formula
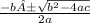`\frac{-b±\sqrt{b^(2)-4ac } }{2a}` to solve for x. *Please ignore the A after b. I cannot remove it for some reason.*

From our equation, a represents the coefficient of the term with degree of 2. Therefore, our a variable is 1. b represents the coefficient of the term with degree 1. Out variable b is therefore -3. Lastly, c represents the term with degree 0. Our c variable is -18. Lets solve!

`\frac{3 ±\sqrt{(-3)^(2)-4*1*(-18) } }{2*1} =\\(3 ±√(9+72) )/(2) =\\(3 ±√(81) )/(2) =\\(3 ±9)/(2) \\\\`

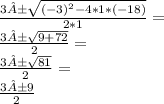
Now we have two possible solutions. Let us start with the addition version:

`(3+9)/(2) =\\(12)/(2) =\\6`

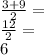
Alternatively you could try the subtraction version:

`(3-9)/(2) =\\(-6)/(2) =\\-12`

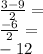
However, the question asks to find the positive solution. Therefore, out answer is 6.

I hope this helps! Please let me know if you have any questions :)