Answer:
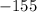
Explanation:
we are given a quadratic function
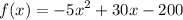
we want to figure out the minimum value of the function
to do so we need to figure out the minimum value of x in the case we can consider the following formula:
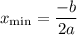
the given function is in the standard form i.e
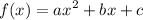
so we acquire:
thus substitute:
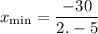
simplify multiplication:
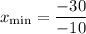
simply division:
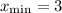
plug in the value of minimum x to the given function:
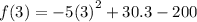
simplify square:
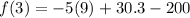
simplify multiplication:
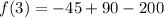
simplify:
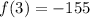
hence,
the minimum value of the function is -155