Expand ( x - 1/x^2)^4

Question

asked Aug 3, 2022 18.5k views

1 Answer

Sinstein · Answer 1 · 2022-08-07T17:55:31+0000

Answer:

We want to expand the expression:

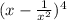
(x - (1)/(x^2) )^4

We can just do it by brute force, this is:

First, rewrite our expression as the product of two square factors:

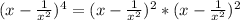
(x - (1)/(x^2) )^4 = (x - (1)/(x^2) )^2*(x - (1)/(x^2) )^2

Now we can expand each one these two factors:

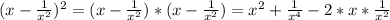
(x - (1)/(x^2) )^2 = (x - (1)/(x^2) )*(x - (1)/(x^2) ) = x^2 + (1)/(x^4) -2*x*(1)/(x^2)

That can be simplified to

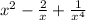
x^2 - (2)/(x) + (1)/(x^4)

Now we can replace that in our original expression to get:

(x^2 - (2)/(x) + (1)/(x^4))*(x^2 - (2)/(x) + (1)/(x^4))

Now we can expand that last product, to get:

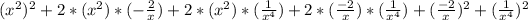
(x^2)^2 + 2*(x^2)*(-(2)/(x) ) + 2*(x^2)*((1)/(x^4)) + 2*((-2)/(x))*((1)/(x^4)) + ((-2)/(x) )^2 + ((1)/(x^4))^2

We can simplify that to:

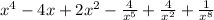
x^4 - 4x + 2x^2 - (4)/(x^5) + (4)/(x^2) + (1)/(x^8)

That is the expanded expression.