1 Answer

Jan Olaf Krems · Answer 1 · 2023-01-03T11:18:43+0000

Given:

In triangle ABC, AB = AC, AD is angle bisector and measure of angle C is 49 degrees.

To find:

The value of x and y.

Solution:

In triangle ABC,

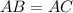AB=AC (Given)

So, triangle ABC is an isosceles triangle and by the definition of base angles the base angles of isosceles triangle are congruent.

In isosceles triangle ABC,

$\angle B\cong \angle C$

$m\angle B\cong m\angle C$

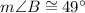
$m\angle B\cong 49^\circ$

The angle bisector of an isosceles triangle is the median and altitude of the triangle. So, the angle bisector is perpendicular to the base.

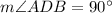
$m\angle ADB=90^\circ$

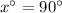
$x^\circ=90^\circ$

In triangle ABD,

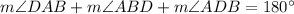$m\angle DAB+m\angle ABD+m\angle ADB=180^\circ$ [Angle sum property]

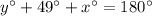
$y^\circ+49^\circ+x^\circ=180^\circ$

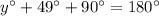
$y^\circ+49^\circ+90^\circ=180^\circ$

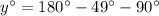
$y^\circ=180^\circ-49^\circ-90^\circ$

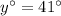
$y^\circ=41^\circ$

Therefore, the correct option is B.

Please log in or register to add a comment.