Question

What is the distance from Cto D?

5
4
D(5,3)
3
2
1
5
1 2 3
C(2, -1
-2
3
-4
-5
OA. 5 units
B. 25 units
C. 7 units
D. 1 unit

Answer 1

Given:

The two points C(2,-1) and D(5,3) on a coordinate plane.

To find:

The distance from C to D.

Solution:

The distance between two points is defined by the distance formula.

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

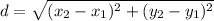
The two points are C(2,-1) and D(5,3). Using the distance formula, we get

`CD=√((5-2)^2+(3-(-1))^2)`

`CD=√((3)^2+(3+1)^2)`

`CD=√((3)^2+4^2)`

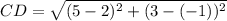
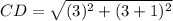
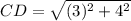
On further simplification, we get

`CD=√(9+16)`

`CD=√(25)`

`CD=5`

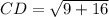
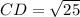
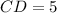
The distance from point C to D is 5 units. Therefore, the correct option is A.