Question

Find the value of X for the given parallelogram

Answer 1

Opposite angles in a parallelogram are congruent

So,

6x-10 = 2x + 50

Now solve like a normal equation

4x = 60
x = 15

Answer 2

• 15

`\:`

Explanation:

Parallelogram is a quadrilateral whose both pairs of opposite sides are parallel and equal and opposite angles are also equal.

`\:`

So,

`\\ { \longrightarrow \qquad{ \pmb{ \sf { \angle P = \angle R}}}} \: \: \\ \\`

`{ \longrightarrow \qquad{ \pmb{ \sf { 6x - 10 = 2x + 50}}}} \: \: \\ \\`

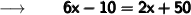
Subtracting 2x from both sides we get :

`\\ { \longrightarrow \qquad{ \pmb{ \sf { 6x - 10 - 2x = 2x + 50 - 2x}}}} \: \: \\ \\`

`{ \longrightarrow \qquad{ \pmb{ \sf { 4x - 10 = 50 }}}} \: \: \\ \\`

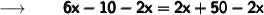
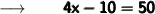
Adding 10 to both sides we get :

`\\ { \longrightarrow \qquad{ \pmb{ \sf { 4x - 10 + 10 = 50 + 10 }}}} \: \: \\ \\`

`{ \longrightarrow \qquad{ \pmb{ \sf { 4x = 60 }}}} \: \: \\ \\`

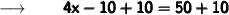
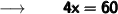
Dividing 4 from both sides we get :

`{ \longrightarrow \qquad{ \pmb{ \sf { (4x)/(4) = (60)/(4) }}}} \: \: \\ \\`

`{ \longrightarrow \qquad{ \pmb{ \frak { x = 15 }}}} \: \: \\ \\`

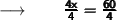
Therefore,

• The value of x is 15