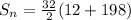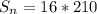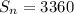Question

Answer each question about the following arithmetic series:

12 + 18 + 24 + 30 + . . . + 198

What is the value of the arithmetic series?

630

1,260

3,360

6,336

Answer 1

(c) 3360

Explanation:

Given

The above arithmetic series where:

`T_1 = 12` --- first term

`d = 6` --- the common difference (18 - 12 = 6)

`T_n = 198` --- The last term

Required

The value of the series

First, we calculate n using:

`T_n = T_1 + (n - 1)d`

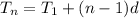
This gives:

`198 = 12 + (n - 1)*6`

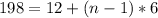
Collect like terms

`198 - 12 = (n - 1)*6`

`186 = (n - 1)*6`

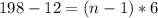
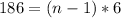
Divide both sides by 6

`31 = (n - 1)`

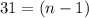
Make n the subject

`n = 31 + 1`

`n=32`

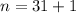
The sum of the series is:

`S_n= (n)/(2)(T_1 + T_n)`

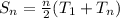
So, we have:

`S_n= (32)/(2)(12 + 198)`

`S_n= (32)/(2)*210`

`S_n= 16*210`

`S_n= 3360`