The probability of choosing a red tile and then a vowel is approximately 4.8%.
To find the probability of choosing a red tile and then a vowel without replacement, we'll follow these steps:
1. Determine the total number of tiles.
2. Find the number of red tiles.
3. Calculate the probability of picking a red tile first.
4. Determine the total number of vowels on the tiles.
5. Calculate the probability of picking a vowel after a red tile has been picked.
6. Multiply the probabilities from steps 3 and 5 to get the compound probability.
From the image, we can identify the tiles and their colors:
- Red Tiles: G
- Blue Tiles: A, K, Q
- Green Tiles: D, R, E
There are a total of 7 tiles.
Step 1: The total number of tiles is 7.
Step 2: There is 1 red tile (G).
Step 3: The probability of picking the red tile first is 1/7.
Step 4: The vowels among the tiles are A and E. There are 2 vowels.
Step 5: After removing the red tile, there are 6 tiles left. The probability of then picking a vowel is 2/6, which simplifies to 1/3.
Step 6: The compound probability is the product of the two probabilities:
P(red tile and then a vowel) = P(red first) × P(vowel second)
P(red tile and then a vowel) =

P(red tile and then a vowel) =
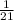
Now, we'll convert this fraction to a percent rounded to the nearest tenth.
![\[ (1)/(21) \approx 0.0476... \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/wmihu53lssyk3ftlmyck4vx8xeb4hqhoyf.png)
To convert to a percent:
![\[ 0.0476... * 100 \approx 4.8\% \]](https://img.qammunity.org/2022/formulas/mathematics/high-school/ic1so3uj7hpjohn2y6isg4l4vohhty0t0y.png)
The answer is approximately 4.8%.