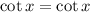Question

[Pre-Calc] Please Help! I don’t know where to start. How do I do this?

Answer 1

See Below.

Explanation:

Problem A)

We have:

`\displaystyle \csc^2\theta \tan^2\theta -1=\tan^2\theta`

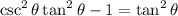
When in doubt, convert all reciprocal trig functions and tangent into terms of sine and cosine.

So, let cscθ = 1/sinθ and tanθ = sinθ/cosθ. Hence:

`\displaystyle \left((1)/(\sin^2\theta)\right)\left((\sin^2\theta)/(\cos^2\theta)\right)-1=\tan^2\theta`

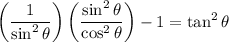
Cancel:

`\displaystyle (1)/(\cos^2\theta)-1=\tan^2\theta`

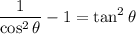
Let 1/cosθ = secθ:

`\sec^2\theta -1=\tan^2\theta`

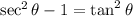
From the Pythagorean Identity, we know that tan²θ + 1 = sec²θ. Hence, sec²θ - 1 = tan²θ:

`\tan^2\theta =\tan^2\theta`

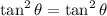
Problem B)

We have:

`\sin^3x=\sin x-\sin x \cos^2 x`

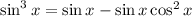
Factor out a sine:

`\sin x(\sin^2 x)=\sin x-\sin x\cos^2 x`

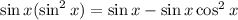
From the Pythagorean Identity, sin²θ + cos²θ = 1. Hence, sin²θ = 1 - cos²θ:

`\sin x(1-\cos^2 x)=\sin x-\sin x\cos^2x`

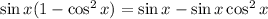
Distribute:

`\sin x- \sin x \cos^2 x=\sin x-\sin x\cos^2 x`

Problem C)

We have:

`\displaystyle (\cos 2x+1)/(\sin 2x)=\cot x`

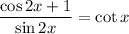
Recall that cos2θ = cos²θ - sin²θ and that sin2θ = 2sinθcosθ. Hence:

`\displaystyle (\cos^2 x-\sin^2 x+1)/(2\sin x\cos x)=\cot x`

From the Pythagorean Identity, sin²θ + cos²θ = 1 so cos²θ = 1 - sin²θ:

`\displaystyle (2\cos^2 x)/(2\sin x\cos x)=\cot x`

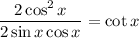
Cancel:

`\displaystyle (\cos x)/(\sin x)=\cot x`

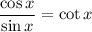
By definition:

`\cot x = \cot x`