Question

1. “Systems of Linear Equations”

American Airlines sold a certain number of tickets from Los Angeles to Hawaii. They charged $90
for flight x and the remaining tickets for $250 for flight y. If the airline sold 120 tickets and
collected a total of $27,600 from the sale of those tickets:
a) Set up the System of Linear Equations
b) How many tickets of each flight were sold?
c) How much money was made from each flight?

Answer 1

Part A)

`\begin{aligned} x+y&=120 \\ 90x+250y&=27600\end{aligned}`

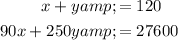
Part B)

Flight X sold 15 tickets and Flight Y sold 105 tickets.

Part C)

Flight X made $1,350 and Flight Y made $26,250.

Explanation:

Let the amount of tickets sold by Flight X be represented by x and the amount of tickets sold by Flight Y be represented by y.

Part A)

The airline sold 120 tickets in total. Hence:

`x+y=120`

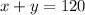
Each x ticket costs $90 and each y ticket costs 250. The total income was $27,600. Thus:

`90x+250y=27600`

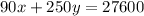
Our system of equations is:

`\begin{aligned} x+y&=120 \\ 90x+250y&=27600\end{aligned}`

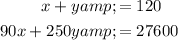
Part B)

Solve the system of equations. We can use substitution. From the first equation, subtract y from both sides:

`x=120-y`

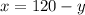
In the second equation, we can divide everything by 10 and substitute in x:

`9(120-y)+25y=2760`

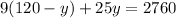
Simplify:

`16y+1080=2760`

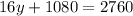
So:

`y=105\text{ tickets}`

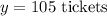
Using the equation above:

`x=120-(105)=15\text{ tickets}`

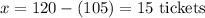
Flight X sold 15 tickets and Flight Y sold 105 tickets.

Part C)

Since each ticket of Flight X sold for $90 and Flight X sold 15 tickets, Flight X made $1,350.

Then it follows that Flight Y made $26,250.