Question

6x + 3y = 6 and 7x + 9y = -22 solve using substitution please

Answer 1

`x=(40)/(11)`

`y=-(58)/(11)`

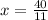
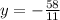
Step-by-step explanation:
`\left \{ {{6x+3y=6} \atop {7x+9y=-22}} \right.`

Multiply both sides of the equation by a coefficient

`\left \{ {{3\left(6x+3y\right)=6*3} \atop {7x+9y=-22}} \right.`

Apply the Distributive Property

`\left \{ {{18x+9y=6*3} \atop {7x+9y=-22}} \right.`

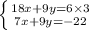
Calculate the product or quotient

`\left \{ {{18x+9y=18} \atop {7x+9y=-22}} \right.`

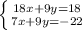
Subtract the two equations

`18x+9y-(7x+9y)=18-(-22)`

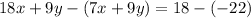
Remove parentheses

`18x+9y-7x-9y=18+22`

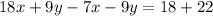
Cancel one variable

`18x-7x=18+22`

Combine like terms

`11x=18+22`

Calculate the sum or difference

`11x=40`

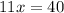
Divide both sides of the equation by the coefficient of variable

`x=(40)/(11)`

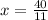
Substitute into one of the equations

`7*(40)/(11)+9y=-22`

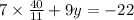
Write as a single fraction

`(7*40)/(11)+9y=-22`

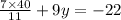
Calculate the product or quotient

`(280)/(11)+9y=-22`

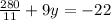
Multiply both sides of the equation by the common denominator

`(280*11)/(11)+9y*11=-22*11`

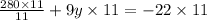
Reduce the fractions

`280+9y*11=-22*11`

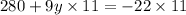
Multiply the monomials

`280+99y=-22*11`

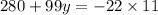
Calculate the product or quotient

`280+99y=-242`

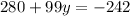
Rearrange variables to the left side of the equation

`99y=-242-280`

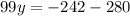
Calculate the sum or difference

`99y=-522`

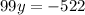
Divide both sides of the equation by the coefficient of variable

`y=-(522)/(99)`

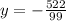
Cross out the common factor

`y=-(58)/(11)`

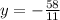
The solution of the system is

`\left \{ {{x=(40)/(11)} \atop {y=-(58)/(11)}} \right.`

I hope this helps you

:)

Answer 2

X = ( 40/11 )

Y = ( -58/11 )

Explanation:

6x + 3y = 6

7x + 9y = -22

-------------------------

-3(6x + 3y = 6)

= -18x - 9y = -18

-------------------------

-18x - 9y = -18

7x + 9y = -22

-11x = -40

÷-11 ÷-11

x = ( 40/11 )

------------------------

6( 40/11 ) + 3y = 6

( 240/11 ) + 3y = 6

-( 240/11 ) -( 240/11 )

3y = ( -174/11 )

÷3 ÷3

y = ( -58/11 )

---------------------------

I hope this helps!