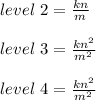Answer:
Following are the responses to the given question:
Step-by-step explanation:
Its machine slows for each further level of evaluation by an n/m factor. Therefore are the times for implementation for levels 2, 3, and 4 are
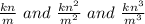 .
.
So, the level values are: