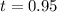Answer:
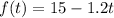

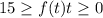
The length of the candle (in inches) 3.6 hours after it was lit is 0.95 inches
Explanation:
Given
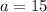 ---- candle length
---- candle length
 --- rate (it is negative because the candle length reduces)
--- rate (it is negative because the candle length reduces)
Solving (a): The function, f(t)
This is calculated as:
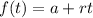
So, we have:

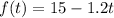
Solving (b): The domain
The domain, in this case, represents time from 0 till the candle burns out.
Set
 to calculate the time the candle burns out
to calculate the time the candle burns out
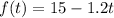

Collect like terms.
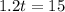
Solve for t
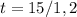

Hence, the domain is:

Solving (c): The range
The domain, in this case, represents the candle height from 15 till the candle burns out (0 inches)
Hence, the range is:
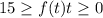
Solving (d):
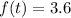
Recall that:
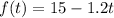
Sp, we have

Collect like terms
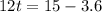
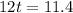
Divide by 12