Question

If $1,000 is deposited in a certain bank account and remains in the account along with any accumulated interest, the dollar amount of interest, I , earned by the deposit in the first n years is given by the formula \small I = 1,000 \left (\left (1+\frac{r}{100} \right )^{n}-1 \right ) , where r percent is the annual interest rate paid by the bank. Is the annual interest rate paid by the bank greater than 8 percent?

Answer 1

The rate is greater than 8%

Step-by-step explanation:

Given

`\small I = 1,000 \left (\left (1+(r)/(100) \right )^(n)-1 \right )`

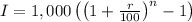
Missing part of question

`I =210`

`n =2`

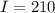
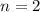
Required

Is r > 1

We have:

`\small I = 1,000 \left (\left (1+(r)/(100) \right )^(n)-1 \right )`

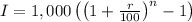
Substitute values for r and I

`210 = 1,000 \left (\left (1+(r)/(100) \right )^(2)-1 \right )`

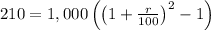
Divide both sides by 1000

`0.210 = \left (\left (1+(r)/(100) \right )^(2)-1 \right )`

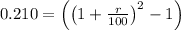
Add 1 to both sides

`1.210 = (1+(r)/(100) \right ))^(2)`

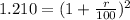
Take square roots of both sides

`√(1.210) = 1+(r)/(100)`

`1.1 = 1+(r)/(100)`

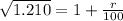
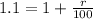
Subtract 1 from both sides

`0.1 = (r)/(100)`

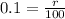
Multiply both sides by 100

`r = 10`

`10 > 8`

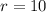
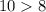
Hence, the rate is greater than 8%