Question

A local police chief claims that about 51% of all drug related arrests are ever prosecuted. A sample of 900 arrests shows that 47% of the arrests were prosecuted. Is there sufficient evidence at the 0.01 level to refute the chief's claim? State the null and alternative hypotheses for the above scenario.

Answer 1

The null hypothesis is
`H_0: p = 0.51`.

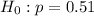The alternate hypothesis is
`H_1: p \\eq 0.51`.

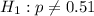The p-value of the test is 0.0164 > 0.01, which means that there is not sufficient evidence at the 0.01 level to refute the chief's claim.

Explanation:

A local police chief claims that about 51% of all drug related arrests are ever prosecuted

At the null hypothesis, we test if the proportion is of 51%, that is:

`H_0: p = 0.51`

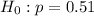
At the alternate hypothesis, we test if the proportion is different from 51%, that is:

`H_1: p \\eq 0.51`

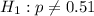
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

0.51 is tested at the null hypothesis:

This means that
`\mu = 0.51, \sigma = √(0.51*0.49)`

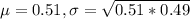
A sample of 900 arrests shows that 47% of the arrests were prosecuted.

This means that
`n = 900, X = 0.47`

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (0.47 - 0.51)/((√(0.51*0.49))/(√(900)))`

`z = -2.4`

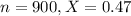
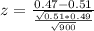
P-value of the test:

Probability that the sample proportion differs from 0.51 by at least 0.04, which is P(|z|>2.4), which is 2 multiplied by the p-value of Z = -2.4.

Looking at the z-table, the Z = -2.4 has a p-value of 0.0082.

2*0.0082 = 0.0164.

The p-value of the test is 0.0164 > 0.01, which means that there is not sufficient evidence at the 0.01 level to refute the chief's claim.