Let Justin's age be x
Let Maggie's age be y
ATQ,
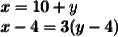
Solve using the substitution method!!
- In this way the equation will be easier to solve because we will get the value of both x and y together...
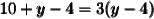
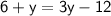
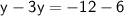
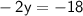
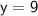
Substitute the value of y into the first equation
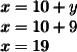
Thus, Maggie's age is 9 and Justin's age is 19...~