The easiest way to find the line parallel to 3x -2y =5 through (1,2), we must set 3x - 2y = 5 into slope-intercept form
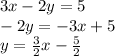
In slope-intercept form, y = mx + b, m is the slope. For two lines to be parallel, their slopes must be equal.
Thus the new line that is parallel to 3x - 2y = 5 must also have a slope of (3/2)x

To find b, we must plug in (1,2)

Thus the equation that is parallel to 3x-2y = 5 and passes through (1,2) is
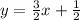
Hope that helps!