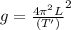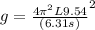Answer:
a)
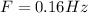
b)

c)

d)

Explanation:
From the question we are told that:
Time
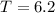
a)
Generally the equation for Frequency F is mathematically given by:
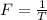

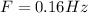
b)
Generally the equation for Frequency F is mathematically given by:
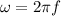
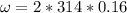

c)
Generally the equation for Length of Chandelier L is mathematically given by:
Since
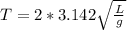
Therefore

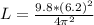

d)
Since
Michelson exhibit except this one swings back and forth 0.11 seconds slower
Therefore
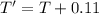
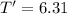
Generally the equation for acceleration due to gravity g is mathematically given by: