Question

Find the SUm of the infinite series.

Answer 1

I'll do problem 13 to get you started.

The expression
`4\left((2^n)/(7^n)\right)` is the same as
`4\left((2)/(7)\right)^n`

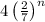
Then we can do a bit of algebra like so to change that n into n-1

`4\left((2)/(7)\right)^n\\\\4\left((2)/(7)\right)^n*1\\\\4\left((2)/(7)\right)^n*\left((2)/(7)\right)^(0)\\\\4\left((2)/(7)\right)^n*\left((2)/(7)\right)^(1-1)\\\\4\left((2)/(7)\right)^n*\left((2)/(7)\right)^(1)*\left((2)/(7)\right)^(-1)\\\\4*\left((2)/(7)\right)^(1)\left((2)/(7)\right)^n*\left((2)/(7)\right)^(-1)\\\\(8)/(7)\left((2)/(7)\right)^(n-1)\\\\`

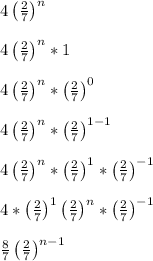
This is so we can get the expression in a(r)^(n-1) form

• a = 8/7 is the first term of the geometric sequence
• r = 2/7 is the common ratio

Note that -1 < 2/7 < 1, which satisfies the condition that -1 < r < 1. This means the infinite sum converges to some single finite value (rather than diverge to positive or negative infinity).

We'll plug those a and r values into the infinite geometric sum formula below

S = a/(1-r)

S = (8/7)/(1 - 2/7)

S = (8/7)/(5/7)

S = (8/7)*(7/5)

S = 8/5

S = 1.6

------------------------

Answer in fraction form = 8/5

Answer in decimal form = 1.6