Answer:
C)
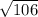 units
units
Explanation:
The Pythagorean Theorem is
 where
where
 and
and
 are side lengths of a right triangle and
are side lengths of a right triangle and
 is the hypotenuse, the longest side of the right triangle.
is the hypotenuse, the longest side of the right triangle.
The distance formula is similar to that of the Pythagorean Theorem which is
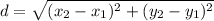 where
where
 and
and
 are the points that you wish to find the distance between them in an (x,y) coordinate plane.
are the points that you wish to find the distance between them in an (x,y) coordinate plane.
Here, we are given that
 is
is
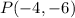 and
and
 is
is
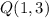 . So, we can use the distance formula as described previously to find the positive distance between the two points:
. So, we can use the distance formula as described previously to find the positive distance between the two points:
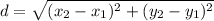
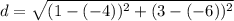

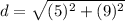

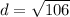
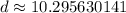
Since all of the given answer choices are in radical form, then C is the correct answer. The distance between the two points is
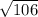 units.
units.