Answer:
60 degrees
Explanation:
The sum of interior angles of a hexagon is 720 degrees, so:
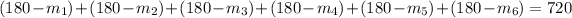
We know that angle 6 is 90 degrees, so:
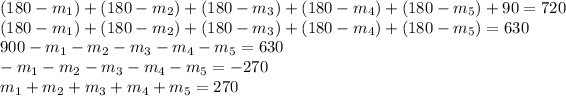
We will rewrite the definition of angle 4:
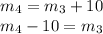
And we will start a substitution madness:
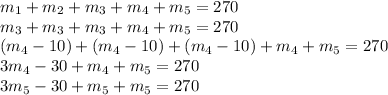
For the sake of simplicity, we will replace angle 5 as x:
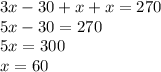
And don't forget the degree sign!