Question

A research center project involved a survey of 846 internet users. It provided a variety of statistics on internet users. (a) The sample survey showed that 94% of respondents said the internet has been a good thing for them personally. Develop a 95% confidence interval for the proportion of respondents who say the internet has been a good thing for them personally. (Round your answers to four decimal places.) 0.9239 Incorrect: Your answer is incorrect. to 0.9561 Incorrect: Your answer is incorrect. (b) The sample survey showed that 67% of internet users said the internet has generally strengthened their relationship with family and friends. Develop a 95% confidence interval for the proportion of respondents who say the internet has strengthened their relationship with family and friends. (Round your answers to four decimal places.) 0.6385 Incorrect: Your answer is incorrect. to 0.7015 Incorrect: Your answer is incorrect.

Answer 1

(a) (0.9240, 0.956)

(b) (0.6383, 0.7017)

Explanation:

The number of internet users involved in the survey, n = 846

The percentage of the respondents that said the internet has been good thing for them personally,
`\hat p` = 94%

(a) The confidence interval of a percentage is given as follows;

`CI=\hat{p}\pm z* \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

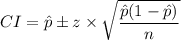
The z-value for 95% confidence interval = 1.96

We get;

`CI=0.94\pm 1.96* \sqrt{(0.94 * (1-0.94))/(846)} \approx 0.94 \pm 1.6003 * 10^(-2)`

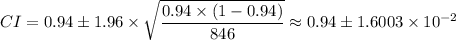
CI = 0.9240 ≤
`\hat p` ≤ 0.956 = (0.9240, 0.956)

(b) The percentage of the internet users that said the internet has directly strengthened their relationship with their families,
`\hat p` = 67% = 0.67

The 95% confidence interval is therefore;

`CI=0.67\pm 1.96* \sqrt{(0.67 * (1-0.67))/(846)} \approx 0.67 \pm 3.1686* 10^(-2)`

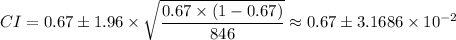
From which we have;

CI = 0.6383 ≤
`\hat p` ≤ 0.7017 = (0.6383, 0.7017)