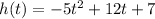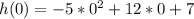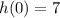Question

The height, h metres, of a springboard diver above the surface of the water t seconds after she leaves the board is given by h=-5t-12+7. Find the maximum height reached by the diver? How long does it take for the diver to reach maximum height? Find the height of the diving board?

Answer 1

`h_(max) = 14.2m`

`t = 1.2`

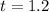
The height of the diver is 7m

Explanation:

Given

`h(t) =-5t^2 + 12t + 7`

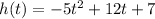
Solving (a): The maximum height reached

First, we calculate the time to reach the maximum height using:

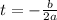`t = - (b)/(2a)` --- maximum of a function

Where

`a = -5; b = 12; c = 7`

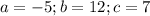
So, we have:

`t = -(12)/(-2 * 5)`

`t = (12)/(10)`

`t = 1.2`

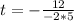
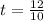
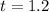
So, the maximum height is:

`h(t) =-5t^2 + 12t + 7`

`h(1.2)=-5 * 1.2^2 + 12 * 1.2 + 7`

`h(1.2)=14.2`

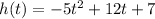
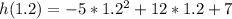
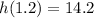
Hence:

`h_(max) = 14.2m`

Solving (b): Time to reach maximum height

This has been calculated in (a)

`t = 1.2`

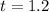
Solving (c): Height of the board.

This can be calculated by setting
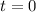`t =0` --- i.e. the height of the diver before diving

So, we have:

`h(t) =-5t^2 + 12t + 7`

`h(0) = -5 * 0^2 + 12 * 0 + 7`

`h(0) = 7`