Answer:
They would know a and b.
a. The mean of this distribution, by the Central Limit Theorem, is the sample mean, and thus, the researches would know this after they took the sample.
b. Sample size is 100 > 30, and thus, by the Central Limit Theorem, they would know that the shape of the distribution is approximately normal.
c. To know the standard deviation of the sampling distribution of the sample mean, the researchers would have to know the population's standard deviation, which they can't get for the sample. So they would not know the standard deviation of the sampling distribution of the sample mean after they took the sample.
Explanation:
Central Limit Theorem
The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean
 and standard deviation
and standard deviation
 , the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
 and standard deviation
and standard deviation
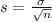 .
.
For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.
For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
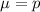 and standard deviation
and standard deviation
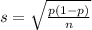
a. The value of the mean of the sampling distribution of the sample mean.
The mean of this distribution, by the Central Limit Theorem, is the sample mean, and thus, the researches would know this after they took the sample.
b. The approximate shape of the sampling distribution of the sample mean.
Sample size is 100 > 30, and thus, by the Central Limit Theorem, they would know that the shape of the distribution is approximately normal.
c. The standard deviation of the sampling distribution of the sample mean.
To know the standard deviation of the sampling distribution of the sample mean, the researchers would have to know the population's standard deviation, which they can't get for the sample. So they would not know the standard deviation of the sampling distribution of the sample mean after they took the sample.