Answer:
The value of the test statistic is z = -0.877.
Step-by-step explanation:
Testing the difference in mean time spent on housework between husbands and wives.
At the null hypothesis, we test if there is no difference, that is, the subtraction of the means is 0:

At the alternate hypothesis, we test if there is a difference, that is, the subtraction of the means is different from 0.

The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis, and s is the standard error.
is the value tested at the null hypothesis, and s is the standard error.
0 is tested at the null hypothesis:
This means that
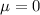
For the wives the mean was 7 hours/week and for the husbands the mean was 4.5 hours/week. The standard deviation of the differences in time spent on house work was 2.85.
This means that
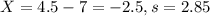
What is the value of the test statistic for testing the difference in mean time spent on housework between husbands and wives?

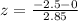
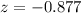
The value of the test statistic is z = -0.877.