Question

Solve for xx. Round to the nearest tenth, if necessary.​

Answer 1

Explanation:

take 58 degree as reference angle

using cos rule

cos 58=adjacent/hypotenuse

0.52=3.6/x

x=3.6/0.52

x=6.92

x=6.9

Answer 2

The length of the base (IJ) in triangle KIJ, given a height (KJ) of
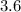`3.6` units, an angle IKJ of
`58` degrees, and a right angle at KJI, is approximately
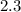`2.3` units.

To solve for the length of the base (IJ = x) in the right-angled triangle KIJ, we can use the tangent function. The tangent of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the adjacent side.

In this case, for angle IKJ (
`58` degrees), the tangent function is given by:

`\[ \tan(58^\circ) = \frac{{\text{height (KJ)}}}{{\text{base (IJ)}}} \]`

Given that KJ =
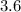`3.6`, we can rearrange the formula to solve for IJ (x):

`\[ x = \frac{{\text{height (KJ)}}}{{\tan(\text{angle IKJ})}} \]`

Substitute the known values:

`\[ x = \frac{{3.6}}{{\tan(58^\circ)}} \]`

Now, calculate this expression to find the length of the base IJ = x. Round to the nearest tenth as necessary.

`\[ x = \frac{{3.6}}{{\tan(58^\circ)}} \]`

Now, let's calculate this expression:

`\[ x = \frac{{3.6}}{{\tan(58^\circ)}} \]`

Using a calculator:

`\[ x \approx \frac{{3.6}}{{1.542}} \]\[ x \approx 2.335 \]`

Therefore, the length of the base (IJ) is approximately
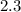`2.3` (rounded to the nearest tenth) units.