Answer:a. 0.13% b. 2.28%
Explanation:
Let x denotes the useful life of batteries.
Given:
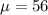 months,
months,
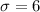
Since X is normally distributed.
The probability that batteries with a useful life of less than 38 months
![P(X<38)=P((X-\mu)/(\sigma)<(38-56)/(6))\\\\=P(Z<-3) \ \ \ [Z=(X-\mu)/(\sigma)]\\\\=1-P(Z<3) \\\\=1- 0.9987\\\\=0.0013](https://img.qammunity.org/2022/formulas/mathematics/college/jvmgo49t7vkxs39fzyig8h5l33gauejxl3.png)
The percent of batteries with a useful life of less than 38 months =0.13%
The probability that batteries will last longer than 68 months
![P(X>68)=P((X-\mu)/(\sigma)>(68-56)/(6))\\\\=P(Z>2) \ \ \ [Z=(X-\mu)/(\sigma)]\\\\=1-P(Z<2)\\\\=1-0.9772=0.0228](https://img.qammunity.org/2022/formulas/mathematics/college/ne05s9yk2kdut9mq3y0lsv9sbsyaznqhho.png)
The percent of batteries that will last longer than 68 months =2.28%