Final answer:
The probability that exactly four customers had their problems solved is 0.250.
Step-by-step explanation:
To find the probability that exactly four customers had their problems solved, we can use the binomial probability formula:
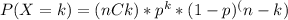
where n is the number of trials, k is the number of successes, p is the probability of success, and (nCk) represents the number of combinations.
For this problem, n = 10, k = 4, and p = 0.70.
Plugging in these values into the formula, we get:
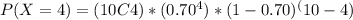
= 0.250