Answer:
The depth to which the hydrometer sinks is approximately 24.07 cm
Step-by-step explanation:
The given parameters are;
The diameter of the hydrometer tube, d = 2.3 cm
The mass of the content of the tube, m = 80 g
The density of the liquid in which the tube floats, ρ = 800 kg/m³
By Archimedes' principle, the up thrust (buoyancy) force acting on the hydrometer = The weight of the displaced liquid
When the hydrometer floats, the up-thrust is equal to the weight of the hydrometer which by Archimedes' principle, is equal to the weight of the volume of the liquid displaced by the hydrometer
Therefore;
The weight of the liquid displaced = The weight of the hydrometer, W = m·g
Where;
g = The acceleration due to gravity ≈ 9.81 m/s²
∴ W = 80 g × g
The volume of the liquid that has a mass of 80 g (0.08 kg), V = m/ρ
V = 0.08 kg/(800 kg/m³) = 0.0001 m³ = 0.0001 m³ × 1 × 10⁶ cm³/m³ = 100 cm³
The volume of the liquid displaced = 100 cm³ = The volume of the hydrometer submerged,
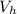
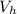 = A × h
= A × h
Where;
A = The cross-sectional area of the tube = π·d²/4
h = The depth to which the hydrometer sinks
h =
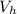 /A
/A
∴ h = 100 cm³/( π × 2.3²/4 cm²) ≈ 24.07 cm
The depth to which the tube sinks, h ≈ 24.07 cm.