Answer:
b. $7732
Explanation:
Value of a depreciating product:
The value of a depreciating product, after t years, is given by:
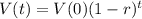
In which V(0) is the initial value and r is the decay rate, as a decimal.
Joe bought a car for $9,000 in 2013. His purchase has depreciated 2.5% every year since then.
This means that
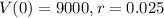 . So
. So
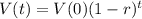
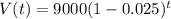
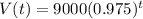
What was his car worth in 2019 to the nearest dollar?
2019 is 2019 - 2013 = 6 years after 2013, so this is V(6).
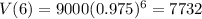
The correct answer is given by option b.