Question

Noah invests $3,600 for two years.

The account pays 0.43% monthly compound interest. To the nearest cent, what's the total that will be in Noah's account after two years?

Answer 1

The total amount in Noah's account after two years is approximately $3672.35.

Step-by-step explanation:

To find the total amount in Noah's account after two years, we can use the formula for compound interest:

`A = P(1 + r/n)^(nt),`

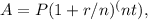
where A is the future amount, P is the principal (initial investment), r is the annual interest rate (0.43% in this case), n is the number of times interest is compounded per year (12 in this case), and t is the number of years (2 in this case).

Substituting the given values, we get:
`A = 3600(1 + 0.0043/12)^(12 * 2)`

Solving this equation, the total amount in Noah's account after two years is approximately $3672.35.

Answer 2

Future value, A = $8444.16

Step-by-step explanation:

Given the following data;

Principal = $3,600

Time = 2 years

Number of times = 24

Interest rate = 0.43 %

To find the future value, we would use the compound interest formula;

`A = P(1 + (r)/(n))^(nt)`

Where;

• A is the future value.
• P is the principal or starting amount.
• r is annual interest rate.
• n is the number of times the interest is compounded in a year.
• t is the number of years for the compound interest.

Substituting into the equation, we have;

`A = 3600(1 + (0.43)/(24))^(24*2)`

`A = 3600(1 + 0.01792)^(48)`

`A = 3600(1.01792)^(48)`

`A = 3600(2.3456)`

Future value, A = $8444.16