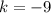Answer:
Explanation:
According to the Polynomial Remainder Theorem, when dividing a polynomial P(x) by a binomial in the form (x - a), the remainder will be given by P(a).
We are given the polynomial:

And it is divided by the binomial:
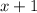
The remainder is 21.
Rewriting the divisor yields:

So, a = -1.
Then by the PRT:
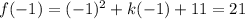
Simplify:
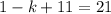
Solve for k: