Answer:
Explanation:
The formula for an explicit geometric sequence is
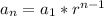 where n is the position of the number in the sequence (ours will be 9 since we are looking for the 9th term), a1 is the first term in the sequence (ours is given as 12), and r is the common ratio (ours is given as -3). Filling all of that in to get the explicit formula we need:
where n is the position of the number in the sequence (ours will be 9 since we are looking for the 9th term), a1 is the first term in the sequence (ours is given as 12), and r is the common ratio (ours is given as -3). Filling all of that in to get the explicit formula we need:
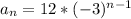 and solving for the 9th term:
and solving for the 9th term:
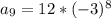 which gives us, simplified a bit:
which gives us, simplified a bit:
 so
so
a9 = 78,732