Question

Oil from a leaking container radiates outwards in the form of a circular film on the water surfaces.

If the area of the circle increases at rate of 900m²/s, how fast is the radius of the circle
increasing when the area is 1400 z m??
[6 marks)
[Ans:3.83m/s]

Answer 1

`(dr)/(dt) = 6.79 \: (m)/(s)`

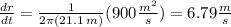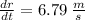
Step by Step Step-by-step explanation:

The area a is defined as

`a = \pi {r}^(2)`

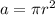
Now take derivative of the above expression with respect to time:

`(da)/(dt) = 2\pi r (dr)/(dt)`

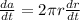
Solving for dr/dt, we then get

`(dr)/(dt) = (1)/(2\pi r) (da)/(dt)`

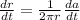
Note that da/dt = 900 m^2/s and when the area of the oil slick is 1400 m^2, the radius r is r = √(1400/π) = 21.1 m. Therefore,the rate at which the radius is increasing dr/dt is

`(dr)/(dt) = (1)/(2\pi(21.1 \: m))(900 \frac{ {m}^(2) }{s} ) = 6.79 (m)/(s)`