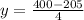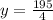Answer:
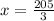
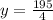
Explanation:
Given
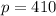 --- perimeter
--- perimeter
See attachment for fence
Required
x and y
The perimeter of the fence is:
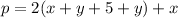
Open bracket

Collect like terms
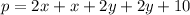

Substitute:
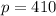

Make 4y the subject
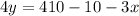
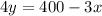
Make y the subject
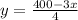
The area (A) of the fence is:
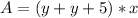
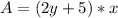
Substitute:
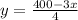
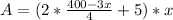
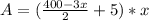
Take LCM

Solve like terms
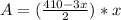
Open bracket
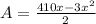
Remove fraction

Differentiate both sides
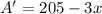
To maximize; set
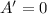

Solve for 3x
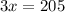
Solve for x
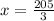
Recall that:
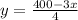
So, we have: