Answer:
hey hope this helps
Comparing sides AB and DE
AB =
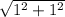

DE
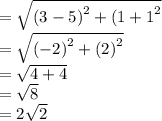
So DE = 2 × AB
and since the new triangle formed is similar to the original one, their side ratio will be same for all sides.
scale factor = AB/DE
= 2
It's been reflected across the Y-axis
moved thru the translation of 3 units towards the right of positive x- axis
for this let's compare the location of points B and D
For both the y coordinate is same while the x coordinate of B is 0 and that of D is 3
so the triangle has been shifted by 3 units across the positive x axis