Question

You play a game where you first choose a positive integernand thenflip a fair coinntimes. You win a prize if you get exactly 2 heads. How should youchoosento maximize your chance of winning

Answer 1

The probability of winning when you choose n is =
`$^nC_2\left((1)/(2)\right)^n$`

`$n\left((n-1)/(2)\right)* \left((1)/(2)\right)^n = n(n-1)\left((1)/(2)\right)^(n+1)$`

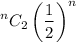
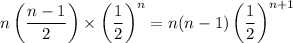
Apply log on both the sides,

`$f(n) = \log\left((n)(n-1)\left((1)/(2)\right)^(n-1)\right) = \log n +\log (n-1)+(n+1) \ \log\left((1)/(2)\right)$`

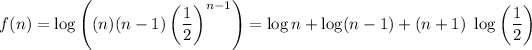
Differentiation, f(x) is
`$f'=(1)/(x)+(1)/((x-1))+\log\left((1)/(2)\right)$`

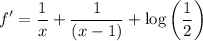
Let us find x for which f' is positive and x for which f' is negative.

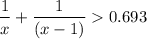`$(1)/(x)+(1)/((x-1)) > 0.693$` , since
`$\log(1/2) = 0.693147$`

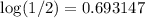
For x ≤ 3, f' > 0 for
`$(1)/(x)+(1)/(x-1)+\log\left((1)/(2)\right)>0$`

`$(1)/(x)+(1)/(x-1)-0.6931470$`

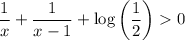
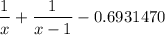
That means f(x) is increasing function for n ≤ 3

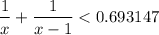`$(1)/(x)+(1)/(x-1)< 0.693147 $` for x > 4

f' < 0 for n ≥ 4, that means f(n) is decreasing function for n ≥ 4.

Probability of winning when you chose n = 3 is
`$3(3-1)\left((1)/(2)\right)^(3+1)=0.375$`

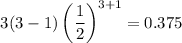
Probability of winning when you chose n = 4 is
`$4(4-1)\left((1)/(2)\right)^(4+1)=0.375$`

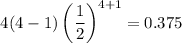
Therefore, we should chose either 3 or 4 to maximize chances of winning.

The probability of winning with an optimal choice is n = 0.375