Question

An object is launched from the top of a building which is 100 m tall (relative to the ground) at a speed of 22 m/s at an angle of 23 degrees BELOW the horizontal. How long, in seconds, does it take to reach the ground

Answer 1

`3.58\:\mathrm{s}`

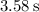
Step-by-step explanation:

We can use the kinematics equation
`\Delta y=v_it+(1)/(2)at^2` to solve this problem. To find the initial vertical velocity, find the vertical component of the object's initial velocity using basic trigonometry for right triangles:

`\sin28^(\circ)=(y)/(22),\\y=22\sin28^(\circ)=10.3283743813\:\mathrm{m/s}`

Now we can substitute values in our kinematics equation:

• 
  `\Delta y=-100`
• 
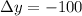
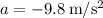  `a=-9.8\:\mathrm{m/s^2}` (acceleration due to gravity)
• 
  `v_i=-10.3283743813\:\mathrm{m/s}`
• Solving for
  `t`

`-100=-10.3283743813t+(1)/(2)\cdot -9.8\cdot t^2,\\\\-4.9t^2-10.3283743813t+100=0,\\\\\boxed{t=3.5849312673637455}, t=-5.692762773751501\:\text{(Extraneous)}`